Deformation and rupture of solids
and evolution of other complex systems
I was a professor of Condensed Matter Physics at Grenoble University. The main goal of my research was to understand deformation and rupture processes in solids, combining experiments or observations in the one hand, and theoretical modeling on the other hand.
Then, I gradually started using theoretical tools from physics of complex systems (and in particular the theory of dynamical systems), to deformation and failure problems in materials physics and in geophysics. including snow avalanches. I recently applied these tools to theoretical studies of climate change and of epidemic growth.
Learn more about my research and areas of study below.
My Work
Collective effects in dislocation dynamics in crystal plasticity.
2006
Example of the Hall-Petch law, revisited in terms of collective dislocation dynamics. The figure shows yield stress vs (grain size)^-1/2. The system gradually departs from the classical case (straight line) as lattice friction goes up (Louchet, Weiss & Richeton, Physical Review Letters 97, 075504 (2006)).
Another example deals with Andrade creep, also revisited in terms of long range elastic interactions (Louchet & Duval, Int. J. for Mat. Research, Special Crussard issue, 2008)
Climate tipping
2016
Using in a simple way the theory of non linear dynamical systems, we show that increasing climatic instabilities may be a qualitative warning sign for the occurrence of a nearby bifurcation, yielding a discontinuous and sudden climate tipping towards an unknown and unpredictable state. The possibility of an accurate prediction of the occurrence time of such a transition is also discussed in terms of the approach of a critical point.
Snow avalanches
2020
This work is a critical update of the most recent and innovative developments of the avalanche science. It aims at re-founding it on clear scientific bases, from field observations and experiments up to strong mathematical and physical analysis and modeling. It points out snow peculiarities, regarding both static mechanical properties and flow dynamics, that may strongly differ from those of compact solids for the former, and of Newtonian fluids for the latter. It analyzes the general processes involved in avalanche release, in terms of brittle fracture and ductile plasticity, specific friction laws, flow of healable granular materials, percolation concepts, cellular automata, scale invariance, criticality, theory of dynamical systems, bifurcations, etc. As a result, slab triggering (including remote triggering) can be summarized by the “slab avalanche release in 4 steps” concept, based on weak layer local collapse and subsequent propagation driven by slab weight. The frequent abortion of many incipient avalanches is easily explained in terms of snow grain dynamical healing. Sluffs and full-depth avalanches are also analyzed. Such advances pave the way for significant progress in risk evaluation procedures. In the present context of a speeding-up climate warming, possible evolutions of snow cover extent and stability are also tentatively discussed. We show how, in mountainous areas, the present analysis can be extended to other gravitational failures (rock-falls, landslides) that are likely to take over from avalanches in such circumstances. The text is supported by on-line links to field experiments and lectures on triggering mechanisms, risk management, and decision making.
(Oxford University Press 2020)
Epidemic dynamics
2020, 2021
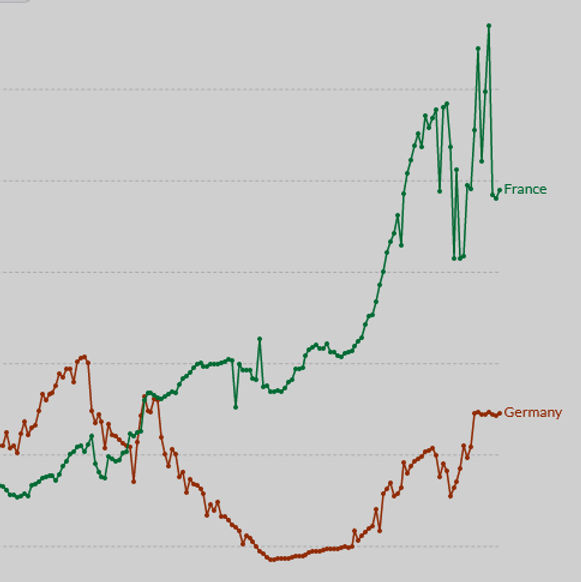
On the basis of the Theory of Dynamical Systems, we proposed a simple theoretical approach for the expansion of contagious diseases (Louchet Biology, june 2020 https://www.mdpi.com/2079-7737/9/6/134/pdf). The infection develops through contacts between contagious and exposed people, with a rate proportional to the number of contagious and of non-immune individuals, to contact duration and turnover, inversely proportional to the efficiency of protection measures, and balanced by the average individual recovery response. The system is shown to converge towards a stable attractor whose value is expressed in terms of the "reproductive rate" Ro, depending on contamination and recovery factors. Various properties of the attractor are examined, and particularly its relations with Ro. As expected, decreasing Ro below 1 leads to a tipping threshold beyond which the epidemic is over. By contrast, increasing Ro values were expected to bring the system through a bifurcating hierarchy of multi-stable cycles up to a chaotic behaviour. Such features (Bi-stable and 4-stable cycles) were discovered in may 2021, appearing as ECGs (electrocardiograms) signals on contamination curves (Louchet, https://www.scitcentralconferences.com/gallery/international-virtual-seminar-on-covid-19
They may be used to renormalize contamination data and associated Ro values between different countries.
A Little About Me
I received an engineering degree at Ecole Nationale Supérieure des Mines (Nancy, France), the "Agrégation" degree in Physics, and a PhD in Solid State Physics. I have been for 30 years Professor of Condensed Matter Physics at Grenoble University (Grenoble Institute of Technology). I was also Invited Professor at Ecole Polytechnique Fédérale de Lausanne (Switzerland), Guest Scientist at McMaster University (Ontario, Canada) and at Los Alamos National Laboratories (USA), OCMR Distinguished Lecturer in McMaster, Toronto, and Kingston Universities (Ontario, Canada), invited scientist at the Balseiro Institute, Bariloche (Argentina) and at Charles University, Prague (Czech Republic). I am a member of the European Physical Society (EPS) and of the French Physical Society (SFP), and the secretary of the Data-Avalanche Association. Now retired, I keep on with my research activity, more particularly on theoretical aspects of instabilities in Physics and Geophysics, but also in Climate Change and in Biology.
